Почему график уравнения Френеля, зависящего от показателя преломления от длины волны, не отображается так, как ожидалось ⇐ Python

[Anonymous]

Я хочу воспроизвести спектр отражения тонкой пленки, комплексный показатель преломления которой зависит от длины волны (данные можно получить здесь). Используя уравнения Френеля для среды 1: воздух, среды 2: тонкая пленка и среды 3: воздух, я написал следующий код:

Код: Выделить всё

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

## Function definition
def Ang_Refrac(na,nb,angle_a):
ang_refrac = np.arcsin( (na/nb).real * np.sin(angle_a) )
return ang_refrac

# Data
Thin_film = pd.read_csv("/content/drive/MyDrive/Python/Si_refractive index.txt", delimiter='\t')

## Variable definition

# espessura do filme fino, [d]: nm
d = 200

# Wave-length
lamb = Thin_film[Thin_film.columns[0]]

# Complex refractive index
N1 = np.ones(len(lamb))
N2 = Thin_film[Thin_film.columns[1]] + Thin_film[Thin_film.columns[1]]*1j
N3 = np.ones(len(lamb))

# Angle:
ang_1_s = 0  #sexagesimais

ang_1 = ang_1_s*np.pi/180  #radianos
ang_2 = [] #radianos
ang_3 = [] #radianos
for i in range(len(N2)):
ang_refrac_12 = Ang_Refrac(N1[i],N2[i],ang_1)
ang_refrac_23 = Ang_Refrac(N2[i],N3[i],ang_refrac_12)
ang_2.append(ang_refrac_12)
ang_3.append(ang_refrac_23)

## Reflectance
R_s = np.zeros(len(lamb))
R_p = np.zeros(len(lamb))

for i in range(len(lamb)):
# S-type polarization
r12_s = (N1[i]*np.cos(ang_1) - N2[i]*np.cos(ang_2[i]))/(N1[i]*np.cos(ang_1) + N2[i]*np.cos(ang_2[i]))
r23_s = (N2[i]*np.cos(ang_2[i]) - N3[i]*np.cos(ang_3[i]))/(N2[i]*np.cos(ang_2[i]) + N3[i]*np.cos(ang_3[i]))

# P-type polarization
r12_p = (N2[i]*np.cos(ang_1) - N1[i]*np.cos(ang_2[i])) / (N2[i]*np.cos(ang_1) + N1[i]*np.cos(ang_2[i]))
r23_p = (N3[i]*np.cos(ang_2[i]) - N2[i]*np.cos(ang_3[i])) / (N3[i]*np.cos(ang_2[i]) + N2[i]*np.cos(ang_3[i]))

# Phase shift
delta = 2 * np.pi * (1/lamb[i]) * d * np.sqrt(abs(N2[i])**2 - (np.sin(ang_1)**2))

# Reflection coefficient
r123_s = (r12_s + r23_s*np.exp(2j*delta)) / (1 - r12_s*r23_s*np.exp(2j*delta))
r123_p = (r12_p + r23_p*np.exp(2j*delta)) / (1 - r12_p*r23_p*np.exp(2j*delta))

# Reflectance
R_s[i] = abs(r123_s)**2
R_p[i] = abs(r123_p)**2

# Reflectance normalization
R_s_normalized = (R_s - min(R_s)) / (max(R_s) - min(R_s))
R_p_normalized = (R_p - min(R_p)) / (max(R_p) - min(R_p))

# Plotting
plt.title("Refletância $\phi=" + str(ang_1_s) + "$°")
plt.xlim(300, 1000)  # Definindo os limites do eixo x
plt.plot(lamb, R_s_normalized, 'go', label="Polarização S", markersize=4)
plt.plot(lamb, R_p_normalized, 'b-', label="Polarização P")
plt.legend()
plt.show()

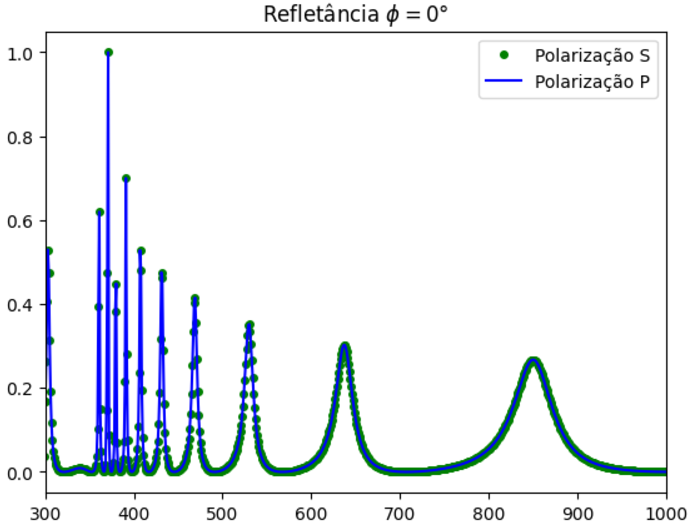
Результирующий график:


Ожидаемый график:


Почему результаты разные?

Подробнее здесь: https://stackoverflow.com/questions/792 ... s-equation